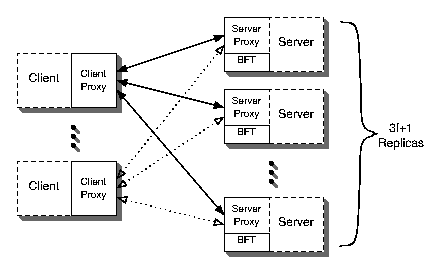
Figure 1: System Architecture
HQ Replication: A Hybrid Quorum Protocol for Byzantine Fault ToleranceJames Cowling1, Daniel Myers1, Barbara Liskov1, Rodrigo Rodrigues2, and Liuba Shrira3 1MIT CSAIL, 2INESC-ID and Instituto Superior Técnico, 3Brandeis University {cowling, dsm, liskov, rodrigo, liuba}@csail.mit.edu |

Figure 1: System Architecture
Figures 2 and 3 show the communication patterns for BFT and HQ; the communication pattern for Q/U is similar to the first round of HQ, with a larger number of replicas. Assuming that latency is dominated by the number of message delays needed to process a request, we can see that the latency of HQ is lower than that of BFT and the latency for Q/U is half of that for HQ. One point to note is that BFT can be optimized so that replicas reply to the client following the prepare phase, eliminating commit-phase latency in the absence of failures; with this optimization BFT can achieve the same latency as HQ. However, to amortize its quadratic communication costs, BFT employs batching, committing a group of operations as a single unit. This can lead to additional latency over a quorum-based scheme.
Figure 5 shows the load at the client. Here we see that BFT-opt has the lowest cost, since a client just sends the request to the replicas and receives a quorum of responses. Q/U also requires one message exchange, but it has larger quorums (of size 4f+1), for 9f+2 messages. HQ has two message exchanges but uses quorums of size 2f+1; therefore the number of messages processed at the client, 9f+4, is similar in HQ to Q/U.
Figures 6 and 7 show the total byte count of the messages processed to carry out a write request. This is computed using 20 byte SHA-1 digests [17] and HMAC authentication codes [16], 44 byte TCP/IP overhead, and a nominal request payload of 256 bytes. We analyze the fully optimized version of Q/U, using compact timestamps and replica histories pruned to the minimum number of two candidates. The results for BFT in Figure 6 show that our optimizations (MACs and preferred quorums) have a major impact on the byte count at replicas. The use of MACs causes the number of bytes to grow only linearly with f as opposed to quadratically as in BFT, as shown by the BFT-MACs line; an additional linear reduction in traffic occurs through the use of preferred quorums, as shown by BFT-opt line.
Based on our analysis, we expect Q/U to provide somewhat less than twice the throughput of HQ at f=1, since it requires half the server message exchanges but more processing per message owing to larger messages and more MAC computations. We also expect it to scale less well than HQ, since its messages and processing grow more quickly with f than HQ's.
Figure 10 shows the performance of HQ for f=1,...,5 in the presence of write contention; in the figure contention factor is the fraction of writes executed on a single shared object. The figure shows that HQ performance degrades gracefully as contention increases. Performance reduction flattens significantly for high rates of write contention because multiple contending operations are ordered with a single round of BFT, achieving a degree of write batching. For example, at f=2 this batching increases from an average of 3 operations ordered per round at contention factor 0.1 to 16 operations at contention factor 1.