Lazy Consistency



Next: Base Algorithm
Up: Lazy Consistency Using
Previous: Related Work
This section defines the kind of consistency our new mechanism
provides.
We refer to the i version of object x as x
version of object x as x . If a transaction
creates a version x
. If a transaction
creates a version x , we assume that it read x
, we assume that it read x .
Transaction T is said to
directly depend on transaction
U if it read x
.
Transaction T is said to
directly depend on transaction
U if it read x and U created version
x
and U created version
x ; we also say that T has read from
U. We say that T depends on U if there exist transactions
V
; we also say that T has read from
U. We say that T depends on U if there exist transactions
V , V
, V ,
,  V
V , where U is V
, where U is V and T is V
and T is V and V
and V directly depends on V
directly depends on V , V
, V directly depends on V
directly depends on V , and so on.
, and so on.
A running transaction Q will view a consistent state if the following
condition is satisfied:
If Q depends on T, it must observe the complete effects of T.
For example, suppose that T creates x and y
and y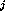 . If Q reads x
. If Q reads x and also
reads y, it must read y
and also
reads y, it must read y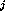 or a version of y that is later than y
or a version of y that is later than y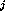 .
.
The same condition is used for providing consistent views for read-only
transactions by Chan and
Gray [7]; that paper proves that if the condition is
satisfied, Q will observe a consistent snapshot of the database. Here we
present a brief synopsis of the proof. Assume T , T
, T , ... T
, ... T is a prefix of the serialization history of the system, where T
is a prefix of the serialization history of the system, where T is the
latest transaction whose updates have been observed by Q. Suppose Q only
depends on transactions T
is the
latest transaction whose updates have been observed by Q. Suppose Q only
depends on transactions T , T
, T , ... T
, ... T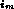 and has
missed the updates of transaction T
and has
missed the updates of transaction T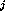 . Since we are ensuring that the
above condition is satisfied for Q, T
. Since we are ensuring that the
above condition is satisfied for Q, T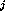 's updates have no impact on
T
's updates have no impact on
T , T
, T , ... T
, ... T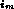 (they do not depend on T
(they do not depend on T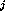 ). If
we consider a history in which we remove (all such) T
). If
we consider a history in which we remove (all such) T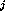 from the set of
committed transactions, there will be no change in the database state
observed by Q. Since a transaction transforms the database from one
consistent state to another and the output of each transaction in
T
from the set of
committed transactions, there will be no change in the database state
observed by Q. Since a transaction transforms the database from one
consistent state to another and the output of each transaction in
T , T
, T , ... T
, ... T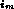 is unaffected by the presence or
absence of T
is unaffected by the presence or
absence of T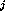 , their combination must yield a consistent database state.
, their combination must yield a consistent database state.
A transaction Q that views a consistent
state is not
necessarily serializable with all the committed transactions in the system.
For example, suppose there are two objects x and y stored at servers X and Y
respectively and suppose that transactions U and
T run in parallel and commit and then Q reads x and y
and y :
:

In this scenario, Q has observed the effects of T but missed
the effects of
U. To commit Q, we would need to serialize it both before U
and after T, but since U is already serialized before T, this is
impossible. The intuition why Q does not observe inconsistencies is
that since T does not depend on U, its modifications must preserve system
invariants regardless of what U does. A possible invariant that might be
preserved is  , where U stores the value of
, where U stores the value of  in
in  and T
increases
and T
increases  .
.
This problem of transaction Q not being serializable can occur only when
there is an anti-dependency: A transaction A anti-depends on B if A
overwrites an object version that B has read. In this case, T anti-depends
on U. Figure 1 shows a cycle that is formed in the
dependency graph [3] for this schedule due to
anti-dependencies.

Figure 1: A non-serializable transaction that has
observed a consistent database state.
Lazy consistency is independent of causality [18]:
a transaction Q might observe the effects of T while missing
the effects of T
while missing
the effects of T , where both T
, where both T and T
and T ran at the same client in
order T
ran at the same client in
order T ; T
; T .
Our implementation
guarantees causality for individual clients, which ensures
that a client always observes the effects of all its previous committed
transactions and the transactions they depended on. We believe such _local
causality_
is good since it means code within a transaction can depend on
invariants holding between objects observed directly and also
results computed by its earlier transactions and stored in local
variables.
Causality is discussed further in
Section 6.3, where we show the additional
cost incurred over lazy consistency to support local causality.
We also show what it would cost to support
_global causality_, in which a client that observes the effects of
transaction T of some other client also observes effects of
all earlier transactions of that client (and the transactions they depended
on).
Note that locking ensures global causality for active transactions.
.
Our implementation
guarantees causality for individual clients, which ensures
that a client always observes the effects of all its previous committed
transactions and the transactions they depended on. We believe such _local
causality_
is good since it means code within a transaction can depend on
invariants holding between objects observed directly and also
results computed by its earlier transactions and stored in local
variables.
Causality is discussed further in
Section 6.3, where we show the additional
cost incurred over lazy consistency to support local causality.
We also show what it would cost to support
_global causality_, in which a client that observes the effects of
transaction T of some other client also observes effects of
all earlier transactions of that client (and the transactions they depended
on).
Note that locking ensures global causality for active transactions.



Next: Base Algorithm
Up: Lazy Consistency Using
Previous: Related Work
Atul Adya
Wed Jun 25 15:09:14 EDT 1997
 version of object x as x
version of object x as x . If a transaction
creates a version x
. If a transaction
creates a version x , we assume that it read x
, we assume that it read x .
Transaction T is said to
directly depend on transaction
U if it read x
.
Transaction T is said to
directly depend on transaction
U if it read x and U created version
x
and U created version
x ; we also say that T has read from
U. We say that T depends on U if there exist transactions
V
; we also say that T has read from
U. We say that T depends on U if there exist transactions
V , V
, V ,
,  V
V , where U is V
, where U is V and T is V
and T is V and V
and V directly depends on V
directly depends on V , V
, V directly depends on V
directly depends on V , and so on.
, and so on.
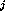 . If Q reads x
. If Q reads x , T
, T , ... T
, ... T and has
missed the updates of transaction T
and has
missed the updates of transaction T and y
and y
 , where U stores the value of
, where U stores the value of  in
in  and T
increases
and T
increases 