 L2
L2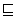 L3
L3 L4. This equation is equivalent to the
two equations
L1
L4. This equation is equivalent to the
two equations
L1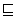 L3
L3 L4
and
L2
L4
and
L2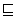 L3
L3 L4, and in
general, we can convert the constraints to a canonical form in which
there is only one label (variable or constant) on the left-hand side.
L4, and in
general, we can convert the constraints to a canonical form in which
there is only one label (variable or constant) on the left-hand side.
6 Verification and Label Inference
This section describes code verification and label inference in more detail. It
demonstrates that basic block labels, labels on local variables,
and labels in declassify expressions can be inferred efficiently and
automatically, making it much more convenient to write properly
annotated code. We present a small example of this process.
As described earlier, procedure verification is a two-step process that first determines basic block labels by propagating the labels of branch-determining expressions, and then checking all the statements in the program in the context of their basic blocks. While the expressions that control branch decisions can be identified statically, their labels depend on the label of the basic block in which they occur. We seem to have a chicken-and-egg problem.
The difficulty can be resolved by creating a label constraint system and solving for all the inferred labels simultaneously. We start by inventing fresh labels Li for each of the branch expressions in blocks Bi. These labels are propagated according to the rules for determining basic block labels, and fed into the statement verification stage. Verifying each statement requires checking of corresponding constraints involving labels. To verify code, we collect all the constraints that are demanded by the various statements, and solve them as a system. If the constraints are inconsistent and generate a contradiction, the program contains an information leak.
Solving the constraint system is tractable because
the constraints all take a particularly simple form.
Each constraint
has either a label or a join of labels on both the left- and right-hand sides,
e.g.,
L1 L2
L2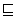 L3
L3 L4. This equation is equivalent to the
two equations
L1
L4. This equation is equivalent to the
two equations
L1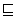 L3
L3 L4
and
L2
L4
and
L2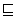 L3
L3 L4, and in
general, we can convert the constraints to a canonical form in which
there is only one label (variable or constant) on the left-hand side.
L4, and in
general, we can convert the constraints to a canonical form in which
there is only one label (variable or constant) on the left-hand side.
Explicitly declared labels (whether constants or first-class labels)
and implicit argument labels are treated as
constants; basic block labels and undeclared labels on local variables
are treated as variables.
The goal of verification is to determine whether there are assignments
to the local variable labels and basic block labels that satisfy all the
constraints. This problem is similar in form to the problem of satisfying
propositional Horn clauses; in fact, a linear-time algorithm for satisfying
Horn clauses [DG84, RM96] can be adapted easily to this problem. If,
on the other hand, we had permitted use of both the  and
and
 operators in
constructing label expressions, the label satisfaction problem would
have become NP-complete [RM96].
operators in
constructing label expressions, the label satisfaction problem would
have become NP-complete [RM96].
The algorithm works by keeping track of conservative upper bounds
for each unknown label. Initially, all the upper bounds are set to
 . The algorithm then iteratively decreases the upper
bounds, until either all equations are satisfied or a contradiction
is observed. At each step, the algorithm
picks an equation that is not satisfied when
all variables are substituted by their upper bounds. If the
unsatisfied equation has a constant label on its left-hand side, a
contradiction has been detected. Otherwise, the upper bound estimate for
the variable label on the left-hand side is adjusted to be the meet
(
. The algorithm then iteratively decreases the upper
bounds, until either all equations are satisfied or a contradiction
is observed. At each step, the algorithm
picks an equation that is not satisfied when
all variables are substituted by their upper bounds. If the
unsatisfied equation has a constant label on its left-hand side, a
contradiction has been detected. Otherwise, the upper bound estimate for
the variable label on the left-hand side is adjusted to be the meet
( ) of its current upper bound and the value of the right-hand
side. In evaluating the right-hand side, all variables are replaced with
their current upper bound estimates.
) of its current upper bound and the value of the right-hand
side. In evaluating the right-hand side, all variables are replaced with
their current upper bound estimates.
Like the algorithm for satisfying Horn clauses, this algorithm requires a number of iterations that is linear in the total size of the constraints; the total size of the constraints is at worst quadratic in the length of the code. Therefore, this inference algorithm seems very practical.
The labels found by this algorithm are the most
restrictive labels that satisfy the constraints. However, the actual
values that the inference algorithm finds are irrelevant, because they
are never converted to first-class values of type label. What is
important is that there is a satisfying assignment to all the labels,
proving that the code is safe.
check_password(db: array[pinfo{ }], user: string,
pwd: string)
returns (ret: bool{user
}], user: string,
pwd: string)
returns (ret: bool{user  pwd
pwd  db})
% Return whether "pwd" is the password of "user"
i: int := 0 %
db})
% Return whether "pwd" is the password of "user"
i: int := 0 %  match: bool := false %
match: bool := false %  while i < db.length() do % L1
if db[i].names = user & % L1
db[i].passwords = pwd then %
match := true % L1
while i < db.length() do % L1
if db[i].names = user & % L1
db[i].passwords = pwd then %
match := true % L1 L2
end %
i := i + 1 % L1
end %
ret := false %
L2
end %
i := i + 1 % L1
end %
ret := false %  if_acts_for(check_password, chkr) %
ret := declassify(match) %
if_acts_for(check_password, chkr) %
ret := declassify(match) %  end
end check_password
end
end check_password
Figure 8 shows the code for a more flexible
version of the check_password procedure that was presented earlier.
This version of check_password is usable by any client principal.
Because the arguments db, user, and pwd have no declared labels,
their labels are implicit parameters to the routine.
Note that the local variables i and result do not explicitly declare
their labels. The resulting
procedure is as safe as the previous version of check_password, and
easier to implement and use.
Let us now walk through the verification process for this code.
The first step in verification is to construct the basic-block diagram
and propagate fresh labels that represent branch expressions. The comments
in Figure 8 show the value of the
basic block labels for each basic block, in terms of the two branch-expression
labels
L1 and L2
(for the if and while, respectively.)
Next, the code is analyzed to generate
the set of label constraints shown in Figure 9,
which include inequalities corresponding to
the statements in the program, plus some equalities that bind the basic-block
branch-expression labels to the labels for the corresponding expressions.
The equalities can be transformed into a pair of
constraints to preserve the canonical constraint form.
Note that the use of declassify generates an additional
constraint, introducing a new variable Ld that represents the
label of the declassified result. This procedure provides a good example
of why it is important for declassification to be able to apply to just
one component of a join, as discussed in Section 3.4.
The fact that declassification works
at all in this procedure, let alone is possible to verify automatically,
is due to this property of the declassification rule.
i := 0

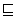
i
match := false

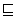
match
while
i
 db
db =
L1
if
i L1 user
user  pwd
pwd  db
db  {chkr: chkr}
{chkr: chkr} 
 pwd
pwd db
db =
L2
match := true
L1  L2
L2
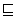
match
i := i + 1
i  L1
L1
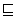
i
ret := false

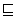
user  pwd
pwd  db
db
declassify
match
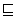
Ld 
{chkr: Ø}
ret := ...
Ld
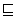
user pwd
pwd db
db
Applying the constraint-solving algorithm described above, a single backward pass through the canonical forms of these constraints yields labels that satisfy them, as shown in Figure 10.
Figure 10: Constraint solutionsi, match, L1,
L2
=
user 
pwd 
db 
{chkr: Ø}
Ld
=
user 
pwd 
db
Next: 7 Related Work Up: A Model for Decentralized Previous: 5 Application to a
Andrew C. Myers, Barbara Liskov