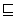 L2, if
L1 has more readers and fewer owners
than L2:
L2, if
L1 has more readers and fewer owners
than L2:
3 Decentralized Information Flow Control
This section describes our new model of decentralized information flow. The model assumes a set of principals representing users and other authority entities. To avoid loss of generality, a process has the authority to act on behalf of some set of principals.
Computations manipulate values. Values are obtained from slots--variables, objects, other storage locations--that can serve as sources and sinks for values, and from computations; values can also be obtained from input channels, which are read-only slots that allow information to enter the system. A value can be written either to a slot or to an output channel, which serves as an information sink that transmits data outside the system.
Values, slots, and channels all have attached labels, which are a more flexible form of the security classes encountered in most information flow models. The flexibility introduced by our labels makes decentralized declassification possible.
The label on a value cannot change, but a new copy of the value can be created with a new label. When this happens we say the value is relabeled, though it is really only the copy that has a new label. The key to secure flow is to ensure that any relabeling is consistent with the security policies of the original labeling. Only values can be relabeled; slots and channels cannot. This restriction allows us to check information flows at compile time. If either slots or channels could be relabeled, we would need run-time label checks whenever they were used.
Sections 3.1 and 3.2 present our new model. Section 3.3 discusses principals in more detail and explains how we achieve flexibility even though slots and channels cannot be relabeled. Section 3.4 defines the relabeling rules, Section 3.5 explains output channels further, and Section 3.6 discusses how our model forms a conventional security-class lattice.
A label L contains a set of principals called the owner set, or owners(L). The owners are the principals whose data was observed in order to construct the data value; they are the original sources of the information. For each owner O, the label also contains a set of principals called the reader set, or readers(L,O). The reader set for a particular owner specifies the principals to whom the owner is willing to release the value. Together, the owners and readers functions completely specify the contents of a label. A useful concept is the effective reader set of L: the set of principals that all owners of the data agree to allow to release it to. The effective reader set is the intersection of the individual reader sets of L.
An example of an expression that denotes a label L is the following: {o1: r1,r2; o2: r2,r3}, where o1, o2, r1, r2 denote principals. The owners of this label are o1 and o2, the reader sets for these owners are readers(L,o1) = {r1, r2} and readers(L,o2) = {r2, r3}, and the effective reader set is {r2}.
This label structure allows each owner to specify an independent flow policy, and thus to retain control over the dissemination of its data. Code running with the authority of an owner can modify the flow policy for the owner's part of the label; in particular, it can declassify that data by adding additional readers. Since declassification applies on a per-owner basis, no centralized declassification process is needed, as it is in systems that lack ownership labeling. The labels maintain independent reader sets for each owning principal. If, instead, a label consisted of just an owner set and a reader set, we would lose information about the individual flow policies of the owners and reduce the power of declassification.
The key to controlling information flow is to ensure that the policies of each owner are enforced as data is read and written. However, when a value is read from a slot, it acquires the slot's label, which means that whatever label that value had at the time it was written to the slot is no longer known when it is read. In other words, writing a value to a slot is a relabeling. This loss of information is acceptable provided there is no loss of control.
Therefore, we allow a value to be assigned to a slot only
if the relabeling that occurs at this point is a restriction,
a relabeling in which the new label
allows fewer accesses than the original; this happens, for example,
if the slot's label allows fewer readers
for an owner than the value's label.
A relabeling from label L1 to label
L2
is a restriction,
written L1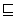 L2, if
L1 has more readers and fewer owners
than L2:
L2, if
L1 has more readers and fewer owners
than L2:
Definition of
L1 |
Note that the rules for readers and owners are opposites.
We could have used a different model in which a slot stores both a value and the label of that value. However, in that model the label that is stored in the slot becomes another information channel. Also, this model would not permit compile-time label checking. Our approach does permit this checking, and therefore labels cause little run-time overhead. As discussed in Section 5, labels can be values themselves; this feature allows label checking to be deferred till run time, overcoming the limitations of doing all checking at compile time.
In addition to slots, the system contains channels, which allow interaction with external devices: input channels allow information to be read and output channels allow information to be written. Reading from an input channel is just like reading from a slot; the value is given the channel's label. However, writing to an output channel is different from writing to a slot; as discussed further in Section 3.5, writing to an output channel is legal if the channel's readers are a subset of the readers allowed by the data being written. Creation of new channels is obviously a sensitive operation.
In this model, it is safe for a process to manipulate data even though the current principal does not have the right to read it. This follows because all the process can do with the data is write it to a slot or a channel provided the data's label allows this. Thus, access-control read checks aren't needed! Nevertheless, such checks might be desired, to reduce the risk of exposure through covert channels of sensitive data such as passwords. One possible extension would be to fold read access checks into label checking: a process can read information from a slot with label L only if the process can act for some principal R in the effective reader set of L.
During computation, values are derived from other values. Since a derived value may contain information about its sources, its label must reflect the policies of each of its sources. For example, if we multiply two integers, the product's label must reflect the labels of both operands.
When a program combines two values labeled with L1 and
L2, respectively,
the result should have the least restrictive label that
maintains all the flow restrictions specified by L1 and
L2. This
least restrictive label, the join of L1 and
L2 (written as
L1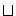 L2,
is constructed as follows:
The owner
set of
L1
L2,
is constructed as follows:
The owner
set of
L1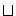 L2
is the union of the owner sets of
L1
and
L2,
and the reader set for each owner in
L1
and
L2
is the intersection of their corresponding reader sets.
This rule can be written concisely, assuming the following natural
definition: readers(L,O) for an O
that is not in the owner set is defined to be
the set of all principals, since O imposes no restrictions on propagation.
The join rule is then the following:
L2
is the union of the owner sets of
L1
and
L2,
and the reader set for each owner in
L1
and
L2
is the intersection of their corresponding reader sets.
This rule can be written concisely, assuming the following natural
definition: readers(L,O) for an O
that is not in the owner set is defined to be
the set of all principals, since O imposes no restrictions on propagation.
The join rule is then the following:
Labels for Derived Values (Definition of
L1
owners(L1 |
(The symbol 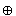 has also been used to denote the join of
two security classes [DD77, AR80].)
has also been used to denote the join of
two security classes [DD77, AR80].)
Note that
L1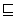 L1
L1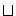 L2
for all labels L1 and L2.
Joining is a restriction and therefore it does not leak information.
L2
for all labels L1 and L2.
Joining is a restriction and therefore it does not leak information.
To allow compile-time analysis, slots must be immutably labeled. Immutable slot labels might seem like a limitation, but we provide two mechanisms to make the labels on slots more flexible: run-time labeling, which is discussed later, and modification of the rights of principals, which changes the set of data that principals can read.
Within a system, principals serve various functions: some represent the full authority of a user of the system; others represent groups of users; and still others represent roles, restricted forms of a user's authority. In practice, these different principals are used quite differently, and many systems treat them as entirely different entities. Some principals have the right to act for other principals and assume their power. For example, every member of a group might have the right to act for the group principal. The acts for relation is reflexive and transitive, defining a hierarchy or partial order of principals. This model is similar to a speaks for hierarchy [LABW91], though roles are treated here as first-class principals. We assume that the principal structure can be queried using the primitive acts-for function to discover whether the current principal has the right to act for another principal.
The right of one principal to act for another is recorded in a database. The database can be modified: for example, to alter the membership of groups, or to transfer a role from one employee to another. Obviously, modifications to the principal structure are extremely powerful and must be restricted by some form of access control. Also, to prevent modifications to the principal structure from serving as a covert channel, the principal database must be labeled in a way that prevents information leaks, just as ordinary databases in the system must be.
This section restates and discusses our two relabeling rules, restriction, which defines the legality of assignment, and declassification, which allows an owner to modify its flow policy:
Rule 1: Restriction. A relabeling from
L1
to
L2
is valid
if it is a restriction:
L1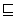 L2.
Intuitively, it removes
readers, adds owners, or both.
L2.
Intuitively, it removes
readers, adds owners, or both.
Rule 2: Declassification. A declassification either adds readers for some owner O or removes the owner O. This relabeling can be done only if the process acts for O.
Relabeling by restriction is independent of the principal hierarchy and requires no special privilege to perform. Declassification, by contrast, depends on the acts-for relation and is legal only when the current process possesses the needed authority. It introduces potential security leaks, but only leaks of information owned by the current principal. The current principal has the power to leak its own information, but cannot leak data owned by other principals. Information that is owned by a particular user can only be declassified by code that runs with that user's authority. Note that Rule 2 reflects the transitivity of the acts-for relation. For example, if a process can act for a principal P, it can act for any principal Q that P can act for, and therefore can declassify data owned by Q.
Analysis of the safety of a piece of code reduces to analysis of the uses of these rules. As we will see, the rules can be largely checked at compile time, assuming the programmer is willing to supply some annotations. Code that performs a relabeling according to Rule 1 can be checked entirely at compile time, but code that performs a relabeling according to Rule 2 requires additional checking, to ensure that the process acts for the owner. In the language discussed later in the paper, we require that the use of Rule 2 be indicated explicitly, since legal but unintended information leaks could occur otherwise.
An important property of these rules is that the join operator does
not interfere with relabeling. It is possible to independently
relabel a component of a join:
if the relabeling
L1  L2.
is legal, then for any other label
L3,
the relabeling
L1
L2.
is legal, then for any other label
L3,
the relabeling
L1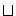 L3
L3  L2
L2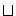 L3
is also legal.
This property automatically holds for Rule 1 because
the set of labels forms a lattice. The property also holds for Rule 2
because the join operator ensures that the flow policies of
L3
are not violated.
L3
is also legal.
This property automatically holds for Rule 1 because
the set of labels forms a lattice. The property also holds for Rule 2
because the join operator ensures that the flow policies of
L3
are not violated.
This property is important because it permits code that is generic with respect to a label (or part of a label) to still perform declassification. It is also helpful for writing code like the statistical analysis package in the medical study example. Because Rule 2 can be applied to part of a join, the analysis package can compute answers using values from its private database, then remove its label from the result that it generates. Without this property, it would have to declassify the private database information immediately--forcing it to give up some protection against leaks in order to perform computation.
Data enters the system through input channels and leaves it through output channels. In either case, it is important that the channel's label reflect reality. For example, if a printer can be read by a number of people, it is important that the output channel to that printer identify all of them, since otherwise an information leak is possible.
Therefore, channel creation is a sensitive operation since it must get the labels right. We assume it is done by trusted code, which makes use of its understanding of the physical devices to determine whether the requested channel should be created, i.e., whether the label proposed by the program attempting to create the channel matches reality. The channel creator might additionally rely on authentication, e.g., when a user logs on, the authentication or login process might associate the user's principal with the channel for the display being used.
A value read from an input channel is labeled with the channel's label. This is the same as what happens when reading a value from a slot. However, the rule for writing to an output channel is different from writing to a slot, since owners don't matter for writing. Instead, the rule is the following: for any reader R of the output channel, the effective readers of the value's label must include a reader R' such that R can act for R'. This rule ensures that the data can read only by readers who have been authorized to see it. The reason to use the acts-for relation is that by authorizing some R', we have implicitly authorized all principals who can act for R'. This flexibility provides functionality not easily attainable through other mechanisms such as declassification. For example, it allows us to write data that is readable by a group principal to a channel that is readable by a member of the group, since the member principal can act for the group principal.
If we consider just Rule 1,
the set of labels forms a conventional security-class
lattice [Den76],
where each element in the lattice is one of the possible labels.
Labels exist in a partial order as defined by the
restriction operator, 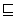 .
The least restrictive label, denoted by
.
The least restrictive label, denoted by  ,
corresponds to data that can flow anywhere; the
greatest restriction,
,
corresponds to data that can flow anywhere; the
greatest restriction,  , corresponds to data that can flow
nowhere: it is readable by no one and owned by everyone. As we go up
in the lattice, labels become strictly more restrictive.
Data can always be relabeled to flow upward in the lattice, because
restriction does not create a possible information leak.
, corresponds to data that can flow
nowhere: it is readable by no one and owned by everyone. As we go up
in the lattice, labels become strictly more restrictive.
Data can always be relabeled to flow upward in the lattice, because
restriction does not create a possible information leak.
The lattice has a well-defined meet operator,  .
Its definition is precisely dual to that of
.
Its definition is precisely dual to that of 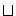 : it takes the
intersection of the owners and the unions of the readers. The meet
operator yields the most restrictive label that is strictly less
restrictive than its operands. This operator doesn't seem to be very
useful in describing computation, and its use is avoided in order to
preserve the ability to easily infer labels, as shown in Section 6.
: it takes the
intersection of the owners and the unions of the readers. The meet
operator yields the most restrictive label that is strictly less
restrictive than its operands. This operator doesn't seem to be very
useful in describing computation, and its use is avoided in order to
preserve the ability to easily infer labels, as shown in Section 6.
The effect of declassification is that each principal has access to certain relabelings that do not accord with the lattice. However, these relabelings do not leak information.
Next: 4 Checking Labels Up: A Model for Decentralized Previous: 2 Motivating Examples
Andrew C. Myers, Barbara Liskov
Copyright ©1997 by the Association for Computing Machinery